Bu yazımızda bir doğrusal denklem sisteminin MATLAB yardımı ile nasıl çözülebileceğini göreceğiz. İlk olarak doğrusal denklemlerden biraz bahsedeğiz ve daha sonra da bu sistemlerin çözümünü MATLAB ile nasıl gerçekleştirebileceğimizi ve ilgili fonksiyonları göreceğiz. Örnek bir sistem verilerek çözümü sağlanacak ve gereken MATLAB kodu yazının geri kalan kısmında sunulacaktır.
Yazı İçeriği
Doğrusal Denklemler
Doğrusal denklemler bir veya birden fazla birinci dereceye sahip değişkenin oluşturduğu ifadelerdir. Üç eğişkenli bir doğrusal denkleme ![]() ifadesi örnek verilebilir. Burada:
ifadesi örnek verilebilir. Burada: ![]() ,
,![]() ve
ve ![]() değerleri sıfırdan farklı sabit değerlerdir. Doğrusal Denklemler özellikle Mühendislik ve Uygulamalı Matematik alanların sıkça kullanılan bir kavramdır.
değerleri sıfırdan farklı sabit değerlerdir. Doğrusal Denklemler özellikle Mühendislik ve Uygulamalı Matematik alanların sıkça kullanılan bir kavramdır.
Doğrusal Denklem Sistemi
Birden fazla doğrusal denklemin oluşturduğu denklem gruplarına Doğrusal Denklem Sistemi denmektedir. Bir doğrusal denklem sisteminin çözülebilmesi için denklemdeki bilinmeyen sayısı kadar denklem setimizin olması gerekmektedir. Üç değişkenli bir Doğrusal Denklem Sistemi düzlemleri temsil eder ve bu düzlemlerin kesişim noktaları da bize çözümü verir.
Örnek:
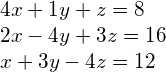
Bu denklem sistemi çözüldüğünde sonuçlarımız ![]() ,
,![]() ve
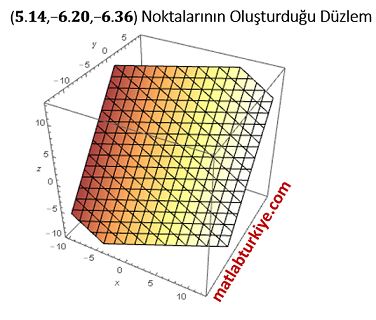
ve ![]() olacaktır ve bu noktalar üç denklemden herbirinin oluşturduğu düzlemin diğer denklemlerin oluşturduğu düzlemler ile kesiştiği noktalardır. Bu bulduğumuz noktalar da bir düzlem oluşturur ve aşağıdaki gibi grafiklendirilebilir.
olacaktır ve bu noktalar üç denklemden herbirinin oluşturduğu düzlemin diğer denklemlerin oluşturduğu düzlemler ile kesiştiği noktalardır. Bu bulduğumuz noktalar da bir düzlem oluşturur ve aşağıdaki gibi grafiklendirilebilir.
Doğrusal Denklem Sistemi MATLAB ile Çözümü
linsolve ile çözüm
linsolve fonksiyonunu kullanarak sistemimizin çözümünü MATLAB ile gerçekleştirebiliriz. Ancak bunu yapmadan önce verilen fonkiyonumuzun ![]() şeklinde olduğundan emin olmalıyız. Diğer bir ifade ile eşitliğin sol tarafında değişkenler sağ tarafınde ise sabitler olmalıdır.
şeklinde olduğundan emin olmalıyız. Diğer bir ifade ile eşitliğin sol tarafında değişkenler sağ tarafınde ise sabitler olmalıdır.
Yukarıda verilen örneği linsolve kullanarak çözelim:
Öncelikle değişkenlerimizi syms fonksiyonu ile sembolik olarak tanımlıyoruz:
syms x y z
Daha sonra denklemlerimizi aşağıdaki şekilde tanımlıyoruz:
denklem1 = 4*x+1*y +z==8; denklem2 = 2*x-4*y+3*z==16; denklem3 = x+3*y-4*z==12;
[adinserter block="2"]
İfademizi ![]() şekline dönüştürerek katsayıları alıyoruz;
şekline dönüştürerek katsayıları alıyoruz;
[A,B] = equationsToMatrix([denklem1, denklem2, denklem3], [x, y, z])
ve de linsolve kullanarak çözümümüzü eldeediyoruz:
X = linsolve(A,B)
Sonuçlarımız komut penceresinde aşağıdaki gibi elde edilir:
X =
36/7
-304/49
-312/49
Dipçe: değişkenlerimizi sembolik olarak tanımladığımız için sonuçlarımız da kesirli olarak geldi.
solve ile çözüm
linsolve alternatifi olarak çözümü solve ile de gerçekleştirebiliriz.
Yine yukarıda olduğu gibi değişkenlerimizi sembolik olarak tanımlar vedenklemlerimizi yazarız:
syms x y z denklem1 = 4*x+1*y +z==8; denklem2 = 2*x-4*y+3*z==16; denklem3 = x+3*y-4*z==12;
Sonrasında da solve komutunu kullanarak çözümümüzü sağlarız:
coz = solve([denklem1, denklem2, denklem3], [x, y, z]); xCoz = coz.x yCoz = coz.y zCoz = coz.z
xCoz =
36/7
yCoz =
-304/49
zCoz =
-312/49