Bu yazıda MATLAB® ile matris işlemlerinde kullanılan temel fonksiyon ve teknikleri bu sayfayı referans alarak göreceğiz.
Temel Matris İşlemlerini görmeden önce en temel olarak bir matris oluşturma ile başlayacağız.
Yazı İçeriği
Matris Oluşturma
Aşağıdaki notasyon ile bir matris oluşturalım:
a = [1 2 3 4 6 4 3 4 5]
Workspace çıktımız aşağıdaki gibi olacaktır.
a =
1 2 3 4 6 4 3 4 5
Şimdi a matrisimizin herbir elementine 2 ekleyelim ve bu sonucu b adında bir matris olarak oluşturalım.
b = a + 2
b =
3 4 5 6 8 6 5 6 7
Görüldüğü üzere MATLAB matris işlemleri yaparken ek bir kod yapısına gereksinim duymaz.
Grafik Çizme
MATLAB ile grafik çizdirmek de bir kod kadar kolaydır. Şimdi b matrisimizin grafiğini ızgaralı grafik yapısı ile bastıralım
plot(b) grid on 
MATLAB ile eksenlere isimler ekleyebileceğiniz gibi diğer grafik türlerini de oluşturabilirsiniz.
bar(b); xlabel('Numune'); ylabel('Agirlik (kg)')
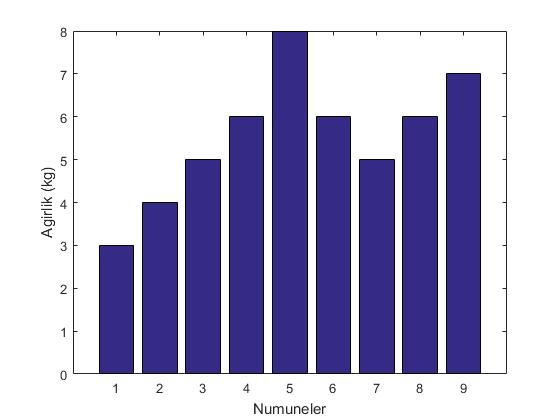
Aşağıdaki örnekteki yıldızlarda görüldüğü gibi MATLAB ile sembollerle de grafil oluşturabiliriz. MATLAB birçok sembol ve çizgi çeşidi sunmaktadır.
plot(b,'*'); axis([0 10 0 10])

MATLAB'in çok başarılı olduğu bir alan da matris hesaplamalarıdır.
Bir matris oluşturmak da bir vektör oluşturmak kadar kolaydır. noktalı virgül (;) kullanarak matris sütunlarını birbirinden ayırabiliriz.
A = [1 2 0; 2 5 -1; 4 10 -1]
A =
1 2 0
2 5 -1
4 10 -1
Tranzpoze (Devrik) Alma
A matrisinin transpozunu (devriğini) de kolaylıkla alabiliriz.
B = A'
B =
1 2 4
2 5 10
0 -1 -1
İki matris çarpımı
Şimdi de bu iki matrisi çarpalım.
Bir kez daha hatırlatalım. MATLAB'te matrisleri belirtmenize gerek yok. MATLAB matrislerle işlem yaparken bunu anlar ve ona göre çözer.
C = A * B
C =
5 12 24
12 30 59
24 59 117
Matris çarpımı yapmak yerine ".*" operatörünü kullanarak iki matrisin birbirlerine karşılık gelen elementlerini de çarpabiliriz..
C = A .* B
C =
1 4 0
4 25 -10
0 -10 1
Şimdi de A matrisini kullanarak A*x = b işlemini çözelim. Bunu da \ (ters taksim) operatörü ile yaparız.
b = [1;3;5]
b =
1
3
5
x = A\b
x =
1
0
-1
Şimdi A*x nin b ye eşit olduğunu görebiliriz.
r = A*x - b
r =
0
0
0
MATLAB neredeyse her çeşit matris işlemi için bir fonksiyona sahiptir.
Özdeğer Bulma
Bir matrisin özdeğerini bulabilmek için aşağıdaki fonksiyonu kullanırız.
eig(A)
ans =
3.7321
0.2679
1.0000
Aynı şekilde tekil değerler için de aşağıdaki fonksiyonu kullanabiliriz.
svd(A)
ans =
12.3171
0.5149
0.1577
"poly" fonksiyonu karakteristik polinomumuzun terim katsayılarını oluşturan matrisi verir.
A matrisinin karakteristik polinomu aşağıdaki gibi olsun,
![]()
p = round(poly(A))
p =
1 -5 5 -1
Polinom Kökü Bulma
Bu polinomun köklerini roots fonksiyonunu kullanarak kolaylıkla bulabiliriz.Bu kökler aslında aynı zamanda matrisimizin de özdeğerleridir.
roots(p)
ans =
3.7321
1.0000
0.2679
Anahtar kelimeler: Matris çarpımı, özdeğer bulma, kök bulma, grafik çizme, matris toplama, matris çıkartma, matris çarpma
tek sütunu olan bir matriste bulunan sıfırları matristen nasıl çıkarabilirim. A=[0;0;1;3;0;5;0]
nonzeros(A) yazarak bulabılirsiniz.