Bisection (İkiye Bölme) Metodu ile Kök Bulma

Bisection (İkiye Bölme) Metodu, bir fonksiyonun köklerini belirli bir alt ve üst limit değerleri arasında bulmaya yarayan bir nümerik yöntemdir. Bu yazımızda ilk önce Bisection metodunu açıklayacağız, daha sonra da verilen bir fonksiyonun köklerini bulmak için MATLAB ile Bisection yönteminin nasıl uygulanacağını göreceğiz.

Bisection (İkiye Bölme) Metodu nedir?

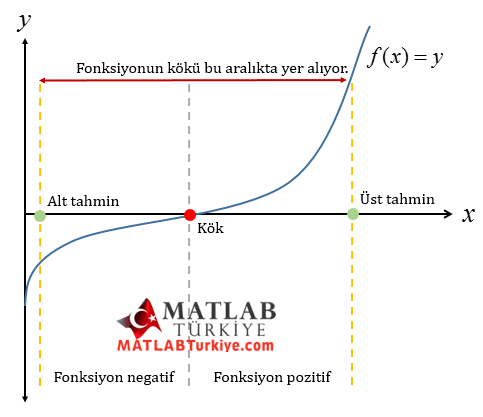
Bir fonksiyonun kökü matematiksel olarak düşünüldüğünde fonksiyon işaretinin değişti noktada yer almaktadır. Bisection Metodunun mantığı da bu işaret değişim noktasını, dolayısı ile de fonksiyonun kökünü girilen alt ve üst tahmin değerleri arasında aramaktır. Girilen tahmin noktaların işaretine bağlı olarak üçüncü orta tahmin noktası alt ve üst tahmin noktalarının ortalaması olarak yazılır. Eğer bu üçüncü orta tahmin noktasının işareti negatif ise yeni alt tahmin noktası olur, eğer işareti pozitif ise yeni üst tahmin noktası olur.

Daha detaylı bilgi için (İngilizce): http://www.mathcs.emory.edu/~cheung/Courses/170/Syllabus/07/bisection.html

Örnek

fonksiyonunun kökünü alt tahmin , üst tahmin ve hata kriteri olacak şekilde Bisection (İkiye Bölme) Metodu'nu kullanarak MATLAB yardımıyla bulalım.

MATLAB Uygulaması – Fonksiyonu Oluşturmak

Öncelikle örneğimizde verilen fonksiyonu MATLAB fonksiyonu olarak yazmamız gerekiyor. Bunun için fonksiyonum isminde bir m dosyası oluşturarak fonksiyonumuzu yazıyoruz.

function [y]=fonksiyonum(x)
y = 5*x.^4 + 2*x.^3 + 10*x-16;

Burada önemli noktamız fonksiyonum.m dosyamızın ismi ile içerisine yazdığımız fonksiyonun da aynı isimde olmasıdır.

MATLAB Uygulaması – Bisection Metodu

Yeni bir m dosyası oluştutarak Bisection Metodumuzu kodluyoruz.

Örneğimizde yer alan değerleri değişken olarak tanımlıyoruz.

clear all; close all; clc;
AT=0;       %Alt tahmin
UT=2;       %Ust tahmin
hata=1e-6;  %Hata değeri

Daha sonra for döngüsü ile Bisection Metodu algoritmamızı yazıyoruz. Burada for döngümüzün maksimum döngü sayısını dolayısı ile de maksimum iterasyon sayısını tanımlıyoruz.

maksit=50;  %Maksimum iterasyon sayısı

for i=1:maksit
    if fonksiyonum(AT)* fonksiyonum(UT) < 0
        M = (AT + UT)/2; %Orta deger
        if fonksiyonum(M)* fonksiyonum(UT) < 0
            AT = M;
        else
            UT = M;
        end
        x(i)=M;
        fx(i)=fonksiyonum(M);
[adinserter block="2"]
        xL(i)=AT;
        xU(i)=UT;
        er(i)=UT-AT;
        %Stopping Criteria
        if (i>1) && (abs(er(i)-er(i-1))<hata)
            break
        end
    end
end

Şimdi de sonuçlarımızı ekrana bastıralım:

%Sonuclari Ekrana Bastiralim
iter=1:1:i;
x=x(1,1:i);
fx=fx(1,1:i);

%Tablo
table=[iter;x;fx;er];
fprintf('\n\niterasyon \t\tx \t\t\t\t\tf(x) \t\t\t\t\t\tHata\n')
fprintf('%2.0f \t\t%2.9f \t\t\t%2.9f \t\t\t\t%2.9f \n',table)

Sonuçlar

Betiğimiz çalışmayı sonlandırdığında sonuçlarımız aşağıdaki gibi çalışma alanına gelecektir.
iterasyon         x                     f(x)                         Hata
1         1.000000000             1.000000000                 1.000000000
2         0.500000000             -10.437500000                 0.500000000
3         0.750000000             -6.074218750                 0.250000000
4         0.875000000             -2.979248047                 0.125000000
5         0.937500000             -1.114669800                 0.062500000
6         0.968750000             -0.090510368                 0.031250000
7         0.984375000             0.446205437                 0.015625000
8         0.976562500             0.175743658                 0.007812500
9         0.972656250             0.042094522                 0.003906250
10         0.970703125             -0.024337974                 0.001953125
11         0.971679688             0.008845701                 0.000976563
12         0.971191406             -0.007754272                 0.000488281
13         0.971435547             0.000543680                 0.000244141
14         0.971313477             -0.003605805                 0.000122070
15         0.971374512             -0.001531190                 0.000061035
16         0.971405029             -0.000493787                 0.000030518
17         0.971420288             0.000024939                 0.000015259
18         0.971412659             -0.000234426                 0.000007629
19         0.971416473             -0.000104744                 0.000003815
20         0.971418381             -0.000039903                 0.000001907
21         0.971419334             -0.000007482                 0.000000954
>>

Sonuçlardan anlayabileceğimiz gibi 21 iterasyon sonrasında hata oranımız sıfıra ve değerimiz de 0.971419334 değerine yakınsamaktadır.