Sabit Kesen Yöntemi (False Position) verilen bir matematiksel fonksiyonun belirli aralıklar arasında kökünü bulmaya yarayan bir Sayısal Analiz yöntemidir. Bisection (İkiye Bölme) Metoduna benzerlik göstermektedir. Ancak Bisection Metodu'nda olduğu gibi 3. tahmini kök değerini bulmak için ilk iki değerin ortalamasını almak yerine, verilen iki tahmin noktasını kesecek şekilde bir doğru çizer ve bu doğrunun x eksenini kestiği nokta başta verilen alt veya üst tahmin değerlerinin yerini alır. Bu yazımızda önce Sabit Kesen Yöntemi'nin mantığından, daha sonra da Sabit Kesen Yöntemi'ni kullanarak örnek bir fonksiyonun kökünü MATLAB yardımıyla bulacağız. Örnek fonksiyonu ve kaynak kodlarını yazının geri kalan kısmında bulabilirsiniz.
Yazı İçeriği
Sabit Kesen Yöntemi (False Position) yöntemi nedir?
Bir fonksiyonun kökü fonksiyon işaretinin değiştiği noktada bulunur. Sabit Kesen Yöntemi (False Position) yönteminin uygulanabilmesi için verilen x değerlerinin fonksiyon değerlerinin zıt işaretli olması gerekir. Böylelikle kökün bu aralıkta olabileceğini söyleyebiliriz.
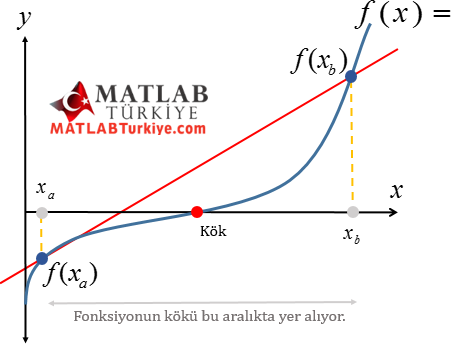
Örneğin 
fonksiyonunun kökünü bulabilmek için verilen iki 
ve 
değerleri arasında kökümüzü bulmak içi bu iki noktanın üzerinden geçecek bir doğru çizeriz ve bu noktanın x eksenini kestiği nokta (
olsun) bizim üçüncü noktamız olur ve ve değerlerinden hangisi ile aynı değere sahip ise onunla yer değiştirir.
noktasını şu şekilde hesaplayabiliriz:
Örnek:
fonksiyonunun kökünü alt tahmin 
, üst tahmin 
ve hata kriteri 
olacak şekilde Sabit Kesen Yöntemi (False Position)'ni kullanarak MATLAB yardımıyla bulalım.
MATLAB Uygulaması
1) Fonksiyon dosyasını oluşturalım
Öncelikle hesaplama sırasında çağıracağımız fonksiyonu oluşturmamız gerekiyor. Bunun için fonksiyonum isminde bir m dosyası oluşturarak içerisine kökünü bulacağımız fonksiyonumuzu yazıyoruz.
function [y]=fonksiyonum(x) y = 4*x.^4 + 6*x.^3 + 10*x-20;
2) Sabit Kesen Yöntemi'ni Uygulayalım
Ekranı temizleyerek başlangıç şartlarımızı yazalım:
clear all; clc; xa=0; xb=2; hata = 1e-9; n=500; %Maksimum iterasyon sayısı
for döngüsü kullanarak oluşturduğumuz Sabit Kesen Yöntemi Algoritmasını çalıştıralım. Döngümüz maksimum iterasyon sayısına kadar Sabit Kesen Yöntemini uygulayacak, sonuçlarımız belirtilen hata kriterini sağladığı zaman da çalışmayı durdurarak sonuçları çalışma alanımıza yazdıracak.
for i=1:n if fonksiyonum(xa)*fonksiyonum(xb) < 0 x2 = (abs(fonksiyonum(xb))*xa + abs(fonksiyonum(xa))*xb)/(abs(fonksiyonum(xa))+abs(fonksiyonum(xb))); if fonksiyonum(x2)*fonksiyonum(xb) < 0 xa = x2; else xb = x2; end %Hata hesabı x(i)=x2; [adinserter block="2"] fx(i)=fonksiyonum(x2); xL(i)=xa; xU(i)=xb; er(i)=xb-xa; %Hata kriteri if (i>1) && (abs(er(i)-er(i-1))<hata) break end end end
Şimdi de döngümüz sonucu bularak tamamlandığında sonuçlarımızı ekrana bastıralım:
%Sonuçları Bastıralım
basamak=1:1:i;
x=x(1,1:i);
fx=fx(1,1:i);
%Tablo
table=[basamak;x;fx;er];
fprintf('\n\nIterasyon \t\tx \t\t\t\t\tf(x) \t\t\t\t\t\tHata\n')
fprintf('%2.0f \t\t%2.9f \t\t\t%2.9f \t\t\t\t%2.9f \n',table)
Sonuç:
Algoritmamız 42 iterasyonun sonunda 0.999999999 değerindeki kökümüze yakınsadı. Farklı fonksiyonlar için kodumuzu çalıştırmak için fonksiyonum.m dosyasını kendi fonksiyonunuza göre düzenleyebilirsiniz.
Iterasyon x f(x) Hata
1 0.303030303 -16.769009066 1.696969697
2 0.524019037 -13.594836857 1.475980963
3 0.683784525 -10.369433578 1.316215475
4 0.795318987 -7.428032098 1.204681013
5 0.870246197 -5.048979373 1.129753803
6 0.918978818 -3.300754360 1.081021182
7 0.949925584 -2.100698684 1.050074416
8 0.969258418 -1.313573284 1.030741582
9 0.981207160 -0.812197304 1.018792840
10 0.988542012 -0.498670498 1.011457988
11 0.993025481 -0.304843254 1.006974519
12 0.995758839 -0.185857278 1.004241161
13 0.997422556 -0.113128883 1.002577444
14 0.998434217 -0.068791557 1.001565783
15 0.999049012 -0.041805523 1.000950988
16 0.999422491 -0.025396401 1.000577509
17 0.999649324 -0.015424584 1.000350676
18 0.999787073 -0.009366896 1.000212927
19 0.999870717 -0.005687770 1.000129283
20 0.999921504 -0.003453557 1.000078496
21 0.999952341 -0.002096901 1.000047659
22 0.999971064 -0.001273155 1.000028936
23 0.999982432 -0.000773000 1.000017568
24 0.999989333 -0.000469327 1.000010667
25 0.999993524 -0.000284950 1.000006476
26 0.999996068 -0.000173006 1.000003932
27 0.999997613 -0.000105040 1.000002387
28 0.999998551 -0.000063774 1.000001449
29 0.999999120 -0.000038720 1.000000880
30 0.999999466 -0.000023509 1.000000534
31 0.999999676 -0.000014273 1.000000324
32 0.999999803 -0.000008666 1.000000197
33 0.999999880 -0.000005261 1.000000120
34 0.999999927 -0.000003194 1.000000073
35 0.999999956 -0.000001939 1.000000044
36 0.999999973 -0.000001178 1.000000027
37 0.999999984 -0.000000715 1.000000016
38 0.999999990 -0.000000434 1.000000010
39 0.999999994 -0.000000264 1.000000006
40 0.999999996 -0.000000160 1.000000004
41 0.999999998 -0.000000097 1.000000002
42 0.999999999 -0.000000059 1.000000001
1 Yorum